In-Memory DBMS 『Peloton』技术简述
这篇文章发表在 2017 VLDB,并且受邀在 2018 年 VLDB 会议上发言
这篇文章初看的时候 有些晦涩 头太疼
简单来说这个题目就是我们在关系数据库中把编译、向量化、预取这些技术都用上了 牛不牛
Motivation
作者这是在向我们要小星星⭐️
hhh 开玩笑的 当然这篇文章的定位确实是 CMU 开源数据库Peloton技术背书
首先 本文研究的是内存数据库的DBMS
内存数据库相较于传统数据库而言
- 数据储存在内存中 读取数据相较于磁盘而言 不可同日而语
- 原来的 Cache 就从内存变成
CPU高速缓存 - 磁盘 I/O 已经 Outer 了,CPU 才是关键(L1,throughput)
- 对于
指针密集型操作(例如 Hash Table,Index Probe)寻址时间占大头 - 所以对提高
缓存覆盖率的需求就很迫切 - 另外在同等 CPU 效力下,提高 CPU 的
计算吞吐量也是一个关键
目前已有的技术可以做到
软件预取Prefetching指令可以在需要之前把数据块从存储器中移动到 CPU 高速缓存中,从而提高缓存覆盖率SIMD-(Single Instruction Multiple Data 单指令多数据)指令利用向量化数据提高计算的吞吐量
但在这篇文章之前还不能把二者结合在一起
上述两者都不适用于a tuple-at-a-time model
- 为了通过预取降低缓存未命中造成的延迟 必须获得大量的元组
- 为了适用 SIMD 把多个维度的向量捆绑在一起 也必须一次获取多个元组
看起来好像都是一次获得多个元组,但二者之间差别很大
- SIMD 要求数据连续打包在一起
- 而预取则不要求预取的地址连续,可以一个个获取
目前支持查询编译的大多数 DBMS 不支持向量化处理或仅仅编译查询一部分,例如宾语,同样没有系统采用数据级并行优化或者预取。
SO 本文的目的就是利用称之为重叠运算符融合的ROF(relaxed operator fusion)模型,使得预取、向量化可以有效的协调工作
Background
在阐述所需要的背景知识之前,先给出一个例子方便理解
TPC-H 是 TPC(Transaction ProcessingPerformance Council)事务处理性能协会用于测试 DBMS 在特定查询下的决策支持能力
TPC-H 中有 22 个子问题 每一个都是较为复杂的语句
本文以 TPC-H Q19 为例子

这是一个两表 Join 操作
回顾一下 SQL Join 操作有
Loop JoinMerge JoinSort Merge JoinHash JoinPartitioned Hash Join等等
各种 Join 有各自的适用条件 其中Merge Join一般用于有序情况,比如说主键的 Join,或者其他索引
而Hash Join比较适用于数据量较大的缺乏索引的等值连接
除了 Loop 和 Merge Join 是有序的操作 之外 其他 Join 都是无序的
而且 Hash Join 需要产生 Hash Table, 建立 Hash Table 的过程是一个需要多次寻址的过程,是一个指针密集的操作
如果没有达到缓存,这个代价还是很大的
Query 编译
DBMS 中编译有两种方式
- 生成.c/.cpp 代码 然后利用外部编译器 gcc,编译为本机代码
- 先用 LLVM 之类的编译器生成中间代码(Intermediate representation) 然后在运行时生成机器代码
除了编译方式的区别 DBMS 中还有几种针对编译的技术
比如说有人提出给每个 operation 建立一个线程 通过调用子线程获得下一个要处理的数据 虽然这样会更快 但 CPU 资源也会消耗的更多
更好的方法就是利用推送的方式 以期减少函数调用次数 简化执行
DBMS 首先识别查询计划中的 pipeline breakers(可以理解为 CPU 刷到内存的一个操作单位,到了这个 Breaker 就会 dump 数据到内存)
在基于推送的模型中 子操作把数据推送给父操作
从一个 pipeline Breaker 到下一个 pipeline breaker 元组数据会 load 到 CPU 寄存器中
两个 breaker 中的任何 operation 就都可以在 CPU 寄存器中完成,从而提高数据局部性
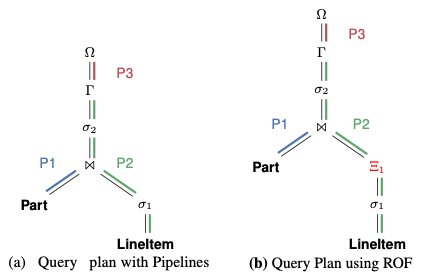
如图(a)所示, 用 P1, P2, P3 三个 Pipeline 表示 TPC-H Q19,用 Ω 表示中间输出表
DBMS 为每一个 pipeline 生成一个 loop 每个 loop 从基表或者中间表读取数据 tuple 然后通过 operation 处理元组
在单个 Loop 中组合多个 operation 称之为运算符融合
显然运算符融合可以较好的提升性能 减少 dump load 而且可以在寄存器中的堆栈中传递元组属性
Hash-Table
Hash Table 是 Hash Join 的产物
另外一张表在遍历时 以 Hash-Table 为判断是否存在对等行(这里也能看出 Hash Table 只能进行等值连接) 从而完成 Join 操作
Hash-Table 在建立时 需要四步 每一步都是依赖上一步的
Hash buck header->Hash buck numberHash Cell address->Hash buck headerBuild tuple->Hash Cell address

Vectorized Processing
CPU 的流水线设计更适合于矢量化计算
上图(b)中所示的就是一种利用向量化的思路处理 TPC-H Q19
不在以每一个 tuple 为粒度 相对而言一次处理一个 Block 中的所有 tuple 这样更好的利用 CPU 资源
Prefetching
内存数据库相较于传统数据库性能提升很大
但是缓存区相较于普通区速度还是差别较大
为了提高效率 尤其是在指针密集型的运算中 由于指针寻址对于读取内存的巨大开销 导致了内存成为性能瓶颈
如果能把所需要的数据在需要之前先 load 进高速缓存 那么就可以大幅度减少因为缓存未命中造成的巨大耗时
Prefetching 可以分为硬件预取和软件预取
硬件预取主要运用在跨步访问模式中 但仅适用于顺序扫描 对于不规则(比如说 Hash-Table)扫描 比较无力
软件预取则有以下几种方式
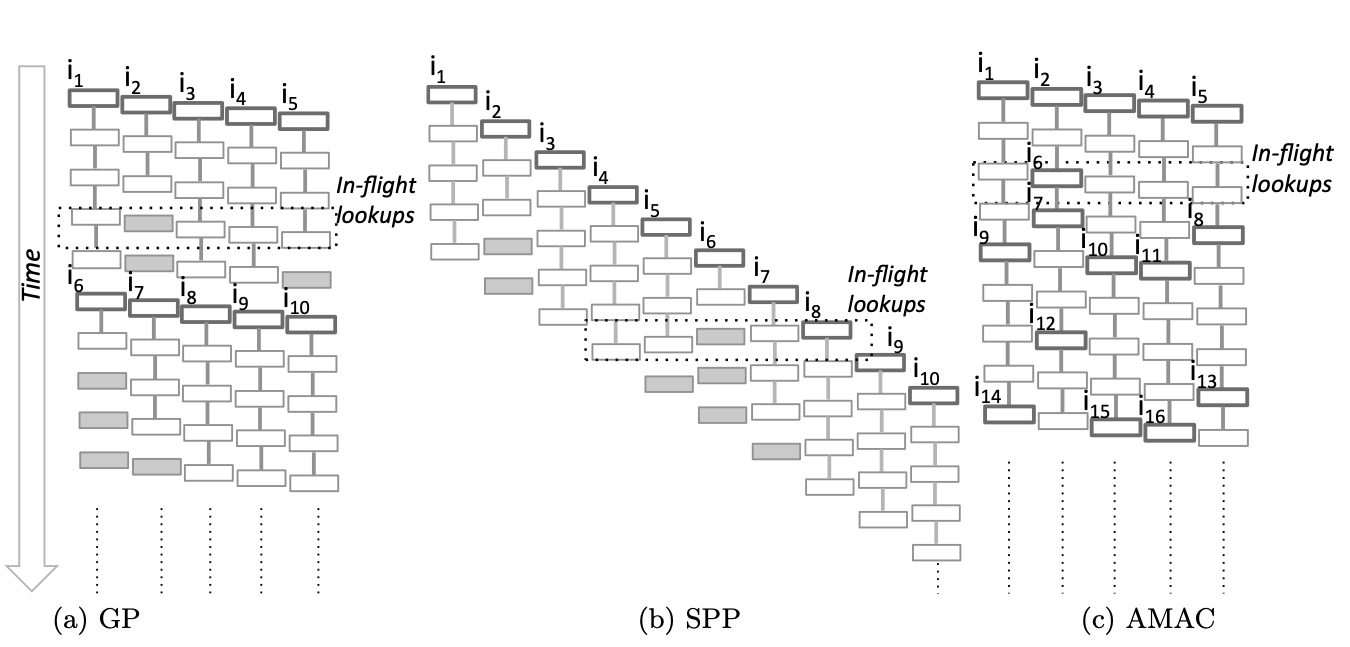
- Group prefetching (GP)
- Software-pipelined prefetching (SPP)
- Asynchronous memory-access chaining(AMAC)
Group prefetching
根据前面可知 Hash-Table 在建立时互相之间存在依赖性 不是很好能预先获得信息
GP-组预取 顾名思义就是分组的形式来预先获取信息
把原来顺序完成的 4 个动作 以组为单位 G 分步完成
在完成 code 0 的时候预取 code 1 的数据 在完成 code 1 的时候预取 code 2 的数据 一次类推
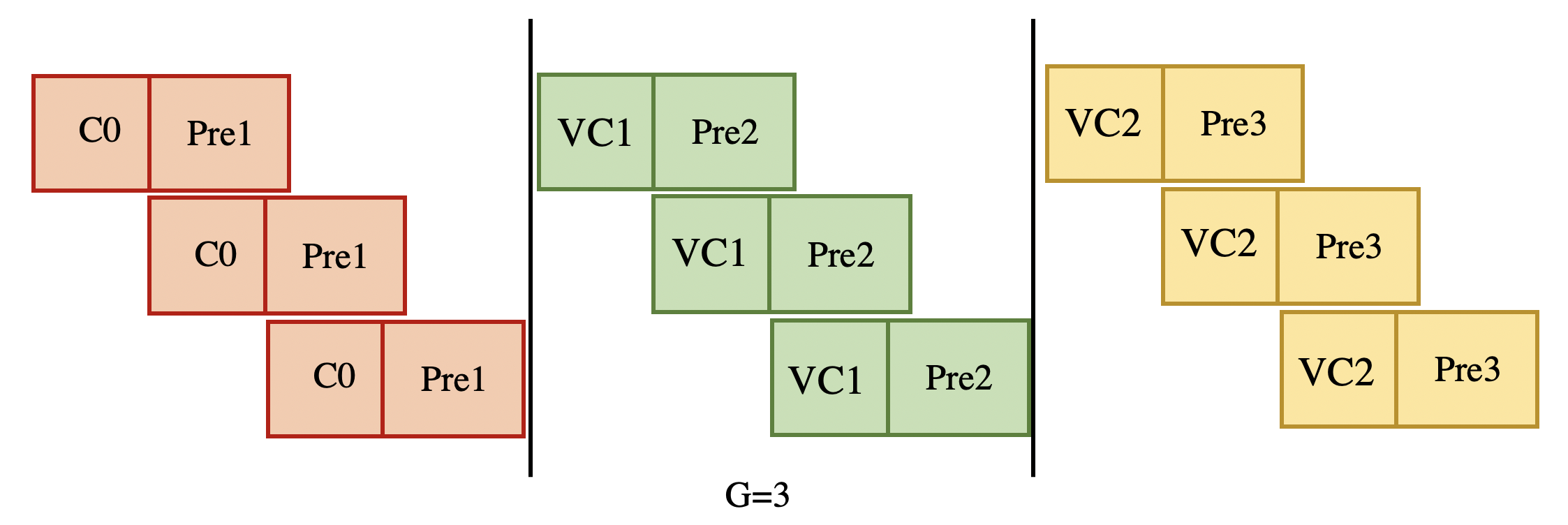
这样只要 G 足够大 就能把从内存 load 到缓存中的时间抵消掉,即
\begin{equation} \left\{\begin{array}{l} (G-1) \cdot C_{0} \geq T_{1} \\ (G-1) \cdot \max \left\{C_{l}, T_{\text {next }}\right\} \geq T_{1}, l=1,2, \cdots, k \end{array}\right. \end{equation}
当然在 Hash-Table 建立的时候 可能会出现冲突 为解决冲突 在访问前加 flag 锁
Software-pipelined prefetching
理解了 GP 那么 SPP 就比较好理解了
我们知道并行有两种一个是时间上的并行 一个是空间上的并行
之前 GP 是按同组分别完成相同的 code 任务 相对于空间上的并行 大家在不同地方做一样的事情
于是就有想法 可以可以利用 CPU 流水线的特性设计出时间上的并行
SPP 就是这样的一种方案
虽然也是一次一组 但这组就不只是完成单一 code 的任务
它依次完成
- 第 j+3D 个 code 0
- 第 j+2D 个 code 1
- 第 j+1D 个 code 3
- 第 j+0D 个 code 4
这样每组都能执行相同的 code 任务 不需要在重复编译程序

同样 只要我们不断增加 D 值 就一定可以找到一个情况 使得并行时间把 load 到缓存的时间抵消掉 从而达到预取的效果
\begin{equation} D \cdot\left(\max \left\{C_{0}+C_{k}, T_{n e x t}\right\}+\sum_{l=1}^{k-1} \max \left\{C_{l}, T_{n e x t}\right\}\right) \geq T \end{equation}
SPP 处理冲突就稍微复杂一点 对于每个冲突的 Hash-Buck 建立相应的消息队列 使得其自动的消费冲突请求
Asynchronous memory-access chaining
虽然在大部分情况下 GP 和 SPP 都能有很好的性能表现
但 GP 不能处理不规则长度的情况 比如说 code k 提前完成 实际查找级数可能少于 N 这就导致必须跳过查找的剩余步骤
当然也可能出现实际级数大于 N 的情况,比如说出现 Hash 冲突 就必须先解决冲突 才能继续进行下去
GP 还会出现读写冲突的情况 比如说 Hash Table 建立时 必须先解决依赖才能下一步操作
所以有学者提出通过构造类似于缓冲池的构建来完成不规则顺序的实现
每次把预取得到的下一个信息丢入缓冲池 然后从缓冲池随机获取下一个需要处理的 code 如此反复
Expanded operation fusion
接着本文就 a tuple a time model, SIMD, a tuple a time + GP 三者做了一次预实验
随着 Hash-Table 的增大 DBMS 性能随之变化 最后得到的结论是 a tuple a time 效果最好
我们使用 operation fusion 最大目标就是最小化物化
物化 这个名词看起来很玄乎 实际上物化可以利用查询中固有的元组并行性
为了达到物化的目的 把 pipeline 分为多个阶段 每个阶段内有多个 operation 融合在一起
管道中各阶段通过缓存中的驻留向量进行通信
由于 ROF 只有一个活动阶段 则可以保证输入、输出向量都在 CPU 的高速缓存
ROF 是 a tuple a time 与 SIMD 之间的混合体
ROF 与 SIMD 最大的区别:
- ROF 总是向下一个阶段提供
完整的向量,而 SIMD 则是可选择限制输入向量的 - 其次
ROF支持跨多个序列operation 的向量化,而 SIMD 则在单个 operation 中运行
以 TPC-Q19 为例,见前(b)图
在σ1之后加了一个 stage,⌅1 表示输出向量
把该 pipeline 分为两个阶段
- 从
LineItem中获取元组并通过过滤器确定其有效性,将其结果添加到stage的输出向量中,直到向量达到容量上限 - 第二个阶段使用此向量来获取有效的
LineItem,以便是的 Hash 能够找到匹配项 如果匹配到了则在σ2中再一次检查其有效性
若能通过 σ2,则在 Ω 聚合
可以注意到每个 pipeline 都对应着一个循环 pipeline 循环内部还存在多个阶段循环,内循环
Vectorization
通常而言 DBMS 不能做到 SIMD
而本文的 ROF 利用 stage 来实现向量化聚集 使得其能提供需要的向量
因为普通的 SQL 不存在 SIMD 所需要的 stage 就有两种想法 来提供这种边界
- operation 突破 SIMD 一次一个迭代 SIMD 的结果 然后传给下一个
- operation 不再迭代单个 pipeline 而是把其结果放在 SIMD 寄存器中传给下一个 operation
然而效果不好 于是本文设定在每个输出阶段上加入 stage
- SIMD 可以提供 100%有效的完整向量
- 使得之后的 operation 不需要再检查有效性
- DBMS 可以专门为 SIMD 生成循环
然后 ROF 利用掩码谓词进行优化
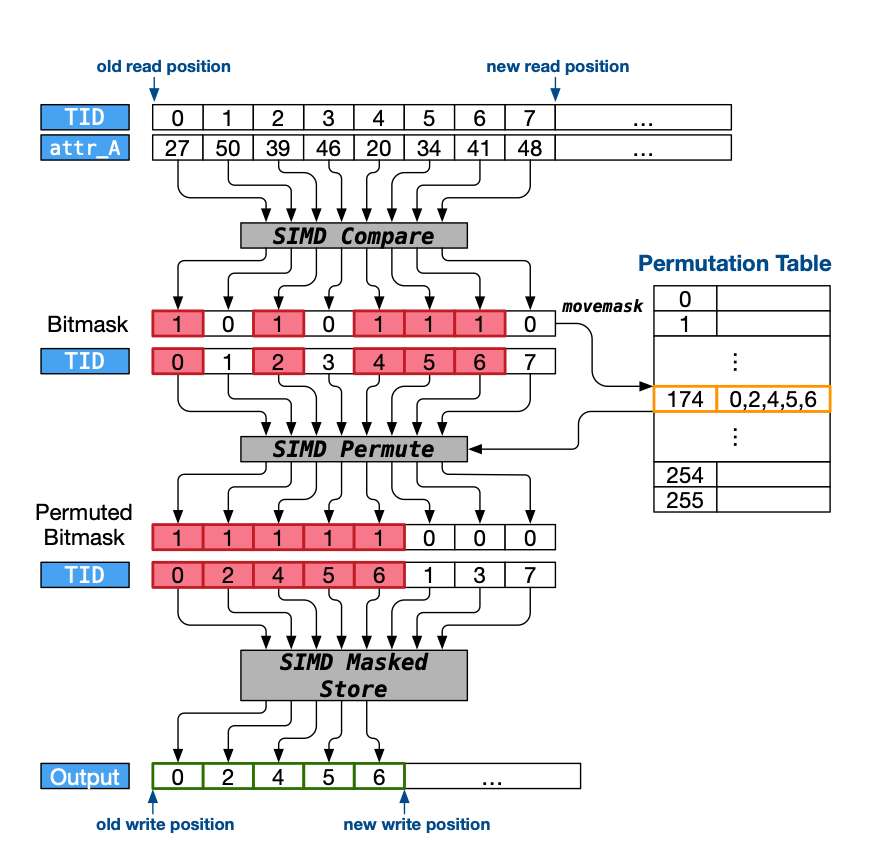
Prefetching
除了顺序访问,内存数据库的 DBMS 存在更为复杂的内存访问
DBMS 必须提前足够多时间来预取,足够抵消内存延迟的时间(当然这部分时间与其他有效的计算相互重叠) 不可避免的是存在预取的开销
如果我们在单个元组中预取数据 这并没有效果
因为单个元组中各个阶段 是相互依赖的 如果知道了这个元组中的下一个指令地址 那么就来不及获取内存延迟
另一方面 积极预取也会认为高速缓存污染和浪费的指令而损失性能
在所有需要的数据大于缓存的 input 阶段加上 stage
这样可以确保启用预取的 operation 接收到完整的输入元组 使得其能重叠计算内存访问
我们选用了MurmurHash3 hash function
- 可以处理多种不同的非整形数据
- 提供多样 Hash 分布
- 快速执行
Hash 表设计为,由一个 8 字节的状态字段开始,其描述了(1)是否为空(2)是否由单个键值对占用(3)是否存在重复键值
重复键值存储在外部连续的存储空间内
通过前加载状态字段和密钥 确保最多只需要 one memory 来检查存储桶是否被占用以及 Hash 值是否匹配
选择GP 最重要的是生成 GP 的代码比较简单
Query Planning
- 是否启用
SIMD - 是否启用预取
如果 SIMD-able 则在 scan 之后添加 Stage
- 查询 operation 依赖的数据量来估计中间表的大小 对需要随机访问大小超过缓存大小的 operation 在输入处 stage 预取
- 在所有执行随机存储的 operation 输入处加 Stage 但一部分预取 一部分不预取
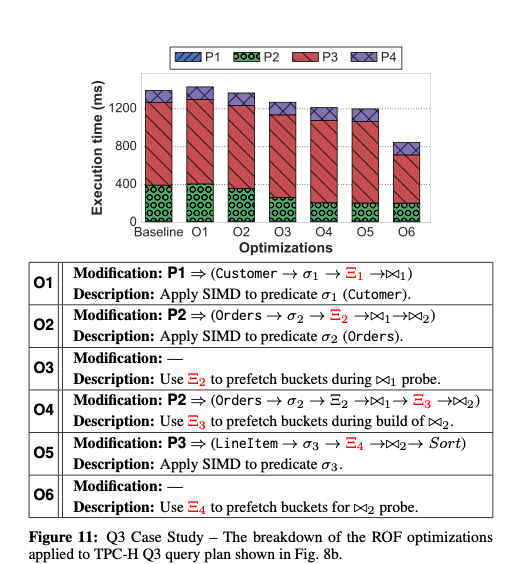
Experiment
使用 Hyper 及其他支持查询编译的 DBMS 进行 TPC-H 测试 并选取了其中八条 进行 针对性的优化 得到不错的结果
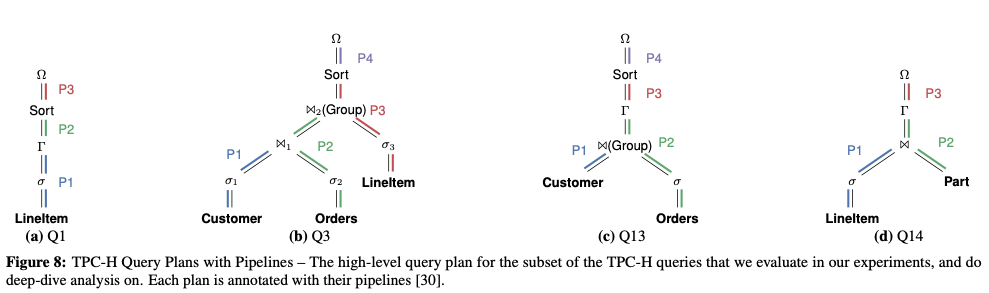
其中 Q13 最能反映优化效果 具体过程就是在一些步骤间增加 Stage 以聚集 SIMD 向量 然后在聚集的过程中 做一些预取操作